In a series of posts I will show you how to make a maze in a wide variety of design constructions. The 40th type of maze construction is the Math maze (a variation of the Number maze). Let’s define what I mean, then get into the example. This maze type is not conducive to outline or shapes so I will use a traditional grid like pattern to illustrate the creation.

Math Maze - A type of number maze where moving from the Start to the Goal is done by correctly answering math problems to move in the correct direction.

HOW TO MAKE A MATH MAZE

Step 1 - Draw the Outline Structure

The outline structure of the math maze should include spaces for math problems with multiple possible pathways branching away from it that will include possible answers. Problems can be housed in circles, bubbles, or any other shape you find interesting. My example includes the most common shape - rectangles. You can download 10 free templates here.

Step 1.5 - Choose the Start and Goal

No surprise these will typically be on opposite ends of most structures. Remember to leave room in the START square for a math problem ! I always make the final space the GOAL with the last answer leading the solver to it.

Step 2 - Start Adding Math Problems

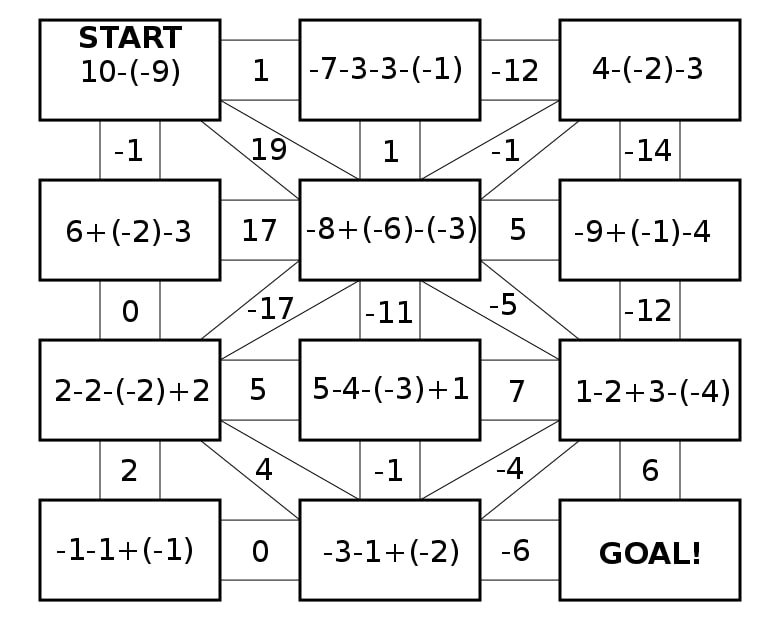
Unlike most mazes, the Math maze starts with a problem in the first square. In my example I use addition and subtraction of positive and negative numbers, a common problem that is easy for anyone to get incorrect, not just new learners (but especially new learners).

Step 3 - Add possible plausible answers

In my example using the addition and subtraction of both positive and negative numbers besides the correct answer there are very common wrong answers. Those should go on the other possible pathways. For the START problem the 3 most common answers are 19 (correct), 1 and -1. If you wanted to lead a student to the correct answer you could use obviously incorrect possibilities like 5 and 7 (but then it would not be challenging). For the second problem there are 8 possible answers (really 7 if you do not consider the path you arrived on). Each number used is a possible answer based on common mistakes so the solver really needs to understand what you are calculating to get the answer correct !

Step 4 - Create the Solution

Make the solution to the maze based on the math problems and correct pathways.

Step 5 - Create False Pathways

Fill in any remaining blocks with incorrect answers, and alternative math problems. If you want to steer students/solvers towards PAST missed answers you can make the false pathways they have taken CORRECT for the next answer by reverse engineering the next math problem, essentially returning them on the pathway they just came from. This will make the student move back and forth between the two problems - hopefully realizing something must be wrong !

3 x 4 math maze using addition and subtraction

Step 6 - (optional) Add Directions

Add directions to explain to the solver how they can move through the maze if you believe it is needed. Most math mazes are self explanatory.

Step 7 - Create a Final Solution

Highlight the correct path in the final version of the maze to create the final maze solution (shown here in gold).

Additional Math Maze Examples

The most difficult thing about making a math maze is the math ! Here is a second example of a Math maze adding in multiplication and division to add difficulty and really test comprehension of the order of operations !

4x3 Math Maze example — Math Maze based on the order of operations rules

Here is a second example of a math maze that is a bit more complicated than it initially looks. All you need to do is move from start to finish, summing each number you pass over. In order to reach the goal correctly you must reach the number 25 exactly from traversing the maze. So while there are no math problems so solve, there is one large math puzzle. The making of this is very different from my step by step instructions above, so it has it’s own How to Make a Math Addition Trail Maze post.

And finally if you are looking for a resource that can help you determine what math problems go with what grade level I suggest you check out the Math Worksheet Center.

For my last example I want to make sure you know about Area Mazes. Called a maze, but actually a type of logic puzzle from Japan created by Naoki Inaba. Used to teach Japan children mathematics and logic. Solving requires calculating the area of a rectangle, often multiple times. Also called Menseki Meiro. If you would like to try to solve some, online area mazes can be found here. Or if you want to read my review of 2 Area Maze books, check this out.

In the below example (you are trying to find the area of the blank box) you would first solve the wall under the # 12. You solve the equation 4 * X = 12. So X = 3, meaning the bottom left side of the square has a length of 3. Now you can solve using the 3 and the 21 to calculate the length of the left side of the square above the 4. Solve 3 * X = 21. The answer is 7. Continue this to solve the Area Maze.

MATH MAZE OR NUMBER MAZE ?

There are a few examples that fall into a grey area between what I call number mazes and what I call Math Mazes. Number Mazes aren’t so much about doing math as counting by a certain number, like 7 in the first example below. You can learn how to make number mazes here. The next 2 examples are probably math mazes but if you called them number mazes I would not fight you. The middle example you need to understand which numbers are divisible by 3 to solve (seems like a math maze to me). The last example you need to know what an even number is and strategically move to a higher even number to solve the maze (number maze?). My point is you can get creative depending on what you are attempting to teach !