We will start this How to with How to Make an Octagon since this will become the base component of the virtually the entire exercise.
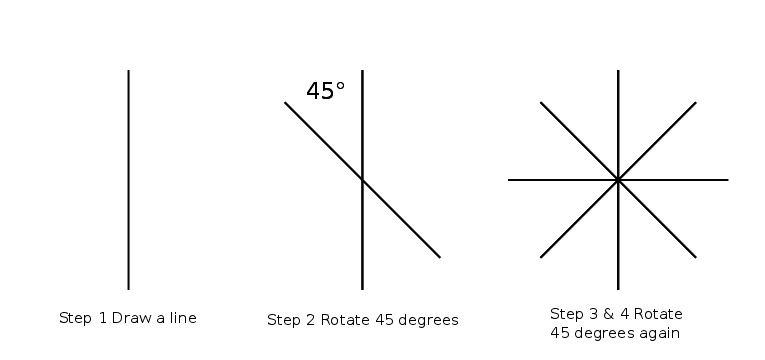
How to Draw an Octagon - Method 1
If you want to draw an octagon with equal lengths here is the method I would use.
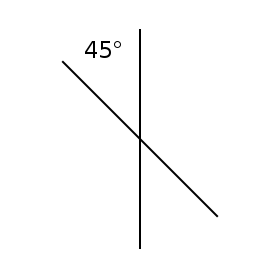
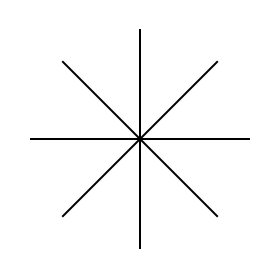
Step 1 Draw a straight line
Step 2 Rotate the line 45 degrees
Obviously this is a digital method where you can copy and paste then rotate, but it also works if you are hand drawing. Use a pencil and protractor/ruler and ensure you use the same length of line.
Step 3/4 Rotate the line twice more at 45 degrees
This will create what looks like an asterisk.
Steps 1-4 to make an octagon
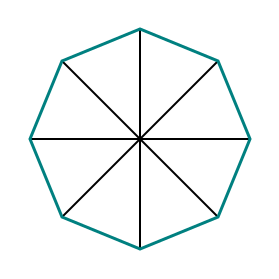
Step 5 Connect the ends of the lines
This will create outer walls of the octagon that are the same length.
Connect the ends of the lines
Step 6 (both optional) Delete the original lines & rotate
After deleting the guidelines, rotate the octagon 22.5 degrees so you have the bottom side flat on the page. I will mention that if you are drawing an octagonal labyrinth you may want to keep the lines to help guide you drawing that (explanation later in the post).
How to Draw an Octagon - Method 2
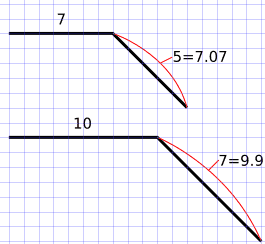
Alternatively you can also use a grid to draw an octagon that is “eyeballed” and has sides that are not quite equal. I will help you some with the math of that and show you how to get your sides very close. If you want to read the full explanation, it is included in the 5 circuit version an includes an Isosceles Right Angle Triangle and calculating the hypotenuse.
We are skipping the math except for the chart below I calculated for you. Basically, if you are using a grid to help you eyeball your octagon, use the highlighted rows. You reverse the lengths from the chart to draw your sides. So a 7 unit grid length is paired with a 5 grid diagonal (which is actually a length of 7.07). Similarly a 10 unit length paired with a 7 grid diagonal (actually length 9.9) also works. So using this math you can draw your own octagonal using grids and 45 degree angles.
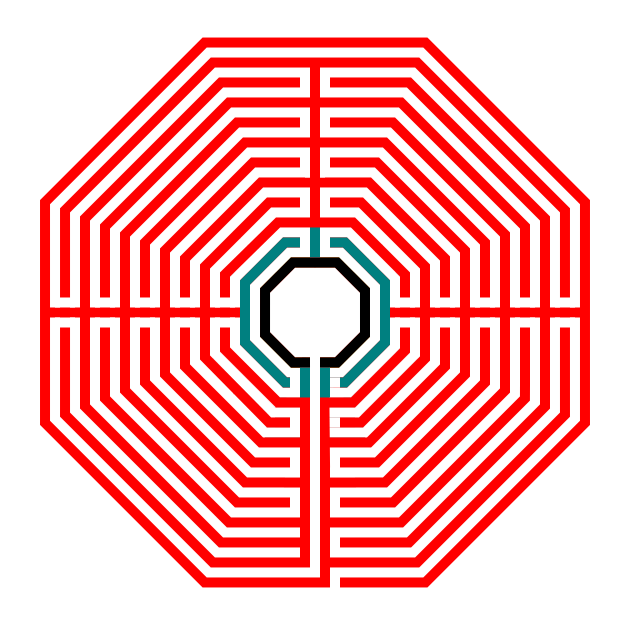
Octagonal Labyrinth pre-how to discussion
When making this labyrinth I suggest you start with the center goal portion and work your way out in layers. Could you design in the opposite direction, from the outside in ? Of course you can ! BUT, you may run out of room for your center goal ! If you go inside out, you only run out of room if you are using a piece of paper that is too small (and digitally you would never run out of room) !!
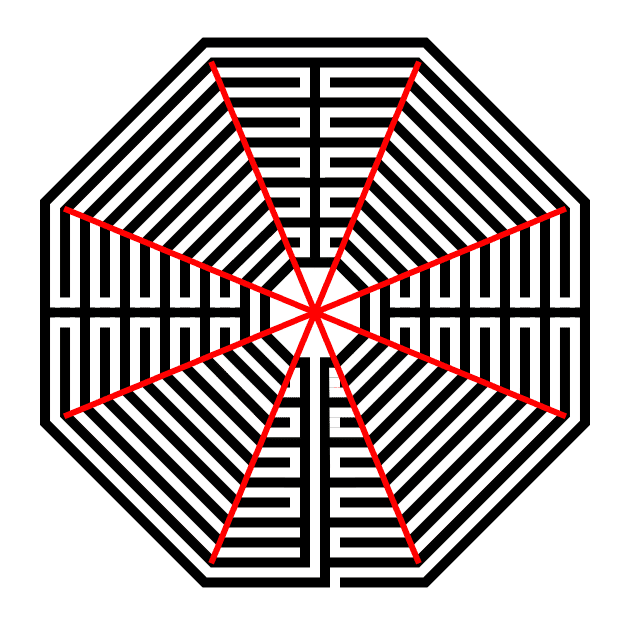
Also I want you to notice where the walls of the labyrinth make their turns. I have highlighted them below in red - If you made your Octagon using Method 1 above you will notice that the walls turn at the exact point it touches the line used to draw the octagon !! Keep this in mind as you draw your labyrinth ! You may also want to keep the original guides with this in mind. That is the reason Step 6 is optional above !
And finally, I prefer to use a standard equal maze construction method where the width of the walls equal the width of the pathways (although you do not need to do the same). I prefer how standard equal objects look.
Note: If you decide to do a standard equal construction I have found it takes some trial and error to get lined up correctly. Using a regular construction will alleviate this.
How to Draw an 11 Circuit Octagon Labyrinth - Method 1
Use this method for drawing a labyrinth without any erasing. It can be made digitally or with a writing utensil. Method 2 is digital and involves drawing and erasing some lines. I prefer Method 2 for digital creations.
Step 1 Draw a Center Octagon (The Goal)
Now that you know how to draw a good octagon let’s get started drawing our labyrinth with one that will create our goal. There is only 1 alteration that you need to make. In the bottom side of the labyrinth, leave a gap in the center for the final pathway. In my example that gap is equal to the width of the line I used to make my octagon.
Step 1 - Draw an octagon (with a gap)
IMPORTANT: From now on the examples will be formed in the following way: Black - previously drawn sections. Blue - current section you are creating. Red - future sections.
Step 2 Draw the first layer from the goal
This layer, shown in blue below consists of what look like brackets on each side of the center. Mine are an equal distance from the initial octagon. However you’ll notice that there are gaps at the top and bottom of the brackets. How do you know where these should start and stop ? For the top of the octagon, draw a centered line equal to 3X width of your walls. The brackets will end 1X width length away from that line (this creates your turnaround point). For the bottom section draw 2 lines down from the entrance to the goal also 3X width of the walls. Again your brackets will end 1X width away from them.
Step 3 Draw the second layer from the goal
This set of brackets is on a north south orientation. To determine where these end, draw a line centered on the right/left side of the previous bracket that measures 2X width. End brackets 1X width away from the these lines. Also, because of the pathway to the goal you will also need to leave a gap in the center of the bottom bracket !
Steps 4-11 Continue drawing each successive layer
We return to the side brackets. We extend our north and south lines by 2X width. We extend and connect our left and right centered lines. Then, we continue to draw each next layer, switching between East/West and North/South brackets.
Step 12 Draw the final outer edge
This final step has some changes to note. In the bottom section of the labyrinth, the the final pathway leading to the goal finally turns into the labyrinth. The only gap is the entrance, directly to the right of the final pathway goal wall. Also note that there is no extension of the wall at due north. This completes the drawing of the octagonal labyrinth.
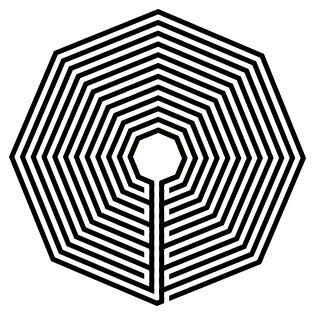
Here is the final version with all lines in black.
How to Draw an 11 Circuit Octagon Labyrinth - Method 2
Step 1 - Draw 12 concentric octagons
Step 2 - Add turnback sections
Once you select how many turn-backs you will have ( my above example has 4 ), draw them, which will typically need one additional line than the # you choose to account for the centered bottom pathway that leads to the goal. The exception is a 1 section labyrinth which needs only 1 turnback.
For a 4 section these will be drawn at 3, 6 , 9 and 12 o’clock. With the extra line occurring at 6 where you create a centered final pathway to the goal. Ensure the lines at 3 and 9 have the innermost pathway open, while 12 has the top pathway open.
Step 3 - Open pathways
At the location of the turn-backs you will need to create the appropriate pathways, along with the entrance and goal pathways. This will create the final labyrinth.
Additional things to consider as you design your own labyrinth
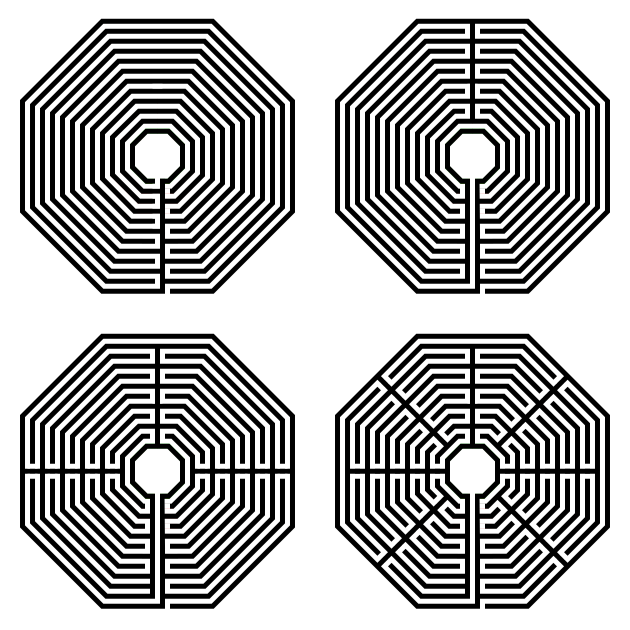
A note about turn-backs. My example above has 4 sections. But you can also draw the same labyrinth with more or less turn-backs (sections). Below I have a 1 section, 2 section, 4 section (the one we just made) and 8 section version. If you imagine walking these, the more sections, or turn-backs, the more back and forth walking you will do.
A note on labyrinth orientation. You also do not need to rotate the octagon you have made, and instead make the labyrinth entrance on a corner. Here is the 1 section version, which of course it could be done like the above in 2, 4, and 8 section versions.
Real World Examples to explore:
A also wanted to give you some information on the most famous octagonal labyrinth in the world, the Amiens Labyrinth in the cathedral in Amiens, France. You can find some great pictures and information about the labyrinth from Atlas Obscura. It has been around since 1288 !
And it has a cousin, as far as labyrinths have cousins I guess, an octagonal labyrinth located in the parish church of the Basilica of Saint-Quentin, in St Quentin, France. It was made sometime around 1495 which makes it both very old, and yet 200 years younger then Amiens !
Additional posts you might like:
The 12 best maze/labyrinth movies of all time